Hannes Birnbacher, Windhagen/Ww.
Rechenschieber & Co.
Womit haben die Leute wohl gerechnet, bevor es Computer gab?
Oh, es ist alles schon mal dagewesen, und es hat keine Batterien gebraucht. Ein handgroßes, viereckiges, flaches Gerät, mit dem man addieren und subtrahieren konnte? Addiator. Eine Vorrichtung, die einem mit ein paar Handbewegungen zeigte, wie viele Jahre man bei fünf Prozent Zins sparen musste, um sein Kapital zu verdoppeln (Eine Simpelfunktion, die den Entwicklern der typischen "kaufmännischen Rechner" bis heute nicht in den Sinn gekommen ist)? Rechenschieber mit doppelt logarithmischen Skalen. Der "Volks"-Rechner für jeden Ladentisch zum Ausmultiplizieren und Rechnung aufaddieren, einfach genug, um in jedem Entwicklungsland aus lokalen Ressourcen gefertigt zu werden? Abakus. Addieren, subtrahieren, Ergebnis auf handelsüblicher Papierrolle ausdrucken? Kurbelrechenmaschine in höchster Entwicklungsstufe von Odhner. Und warum sich mit Quicken, Lexware & Co. abplagen, wenn man Journal und Kontoblätter spaltengenau, je nach Kunden-, Lieferanten- und Sachkonto, mittels einer Buchungsplatte beschriften kann...
Der Addiator

Produx
Nach dem gleichen Prinzip gab's noch viele andere, handliche Addiermaschinen. Hier mein Produx: Eleganz in Kunstleder, für Subtraktion und Addition eingerichtet. Zum Download der Bedienungsanleitung (2-seitig, PDF 125 KB) hier klicken (linke Maustaste).
Rechenschieber

Nichts irritiert die Yuppies in der Hauptversammlung einer
Aktiengesellschaft mehr, als wenn ihr Sitznachbar ein komisches
Lineal
aus der Aktentasche zieht und damit gemächlich die
kompliziertesten
Kennzahlen ausrechnet. Mit etwas vielbeneidetem Geheimwissen
("Potenzen
der Form a hoch n erhält man, indem C-1 über den Basiswert a der
entsprechenden LL-Skala gebracht und der Läufer dann auf C-n
verschoben
wird. Auf LL kann man dann a hoch n ablesen. Z.B. 3,75 hoch 2.96
ist
gleich 50; stelle C-1 über LL3 3.75 und lies bei C-2.96 auf LL3
den
Wert 50 ab", aus der Anleitung zu einem Aristo-Rechenschieber) und
einem guten Richtungssinn, auf welcher Skala man bei Überschreiten
des
linken oder rechten Endes weiterlesen muss, liest der Geübte
Ergebnisse
ab, die der mathematisch nicht so Bewanderte nicht einmal auf
seinem
Handheld herausfindet.
Mancher kennt vielleicht die Parkscheiben, mit denen man die
getankte
Menge den gefahrenen Kilometern gegenüberstellen und den Verbrauch
je
100 km errechnen kann. Dies ist nichts anderes als ein
Rechenschieber
in der Sonderform Rechenscheibe.
Buch: "Rechenschieber - eine Dokumentation"
110 S. , 55 Abb. DM 48.--, oder aber in erweiterter Ausführung
"SLIDE
RULES - A Journey through three centuries", 130 S. 55 Abb.,, mit
Quellenhinweisen, Anmerkungen zu Personen der
Rechenschieber-Geschichte, Index usw. (im Astragal-Verlag, Mendham
,NJ,USA) DM 58.-- , beide zu erfragen bei D.v.Jezierski,
Bahnhofstr.3 , D-90547 Stein.
Die deutsche Version ist herausgegeben im Selbstverlag durch
Herrn v. Jezierski, der vierzig Jahre lang Produktmanager bei
Faber-Castell, Nürnberg für Rechenschieber war und, obwohl
international anerkannter Experte für diese mechanischen
Rechengeräte,
doch , wie ich erlebt habe, heroisch und letztlich
erfolgreich auch mit den Tücken des Computers kämpft, somit unter
vonjezierski.d@debitel.net zu erreichen und
auskunftsbereit ist.
Sammlertreffen: 14.-16.9.2001 in München
Abakus

Ein Holzrahmen mit Stäben, auf die Kugeln geschoben sind, meist eine Unterteilung, um Einerkugeln auf der unteren Hälfte des Stabes, Fünferkugeln auf der oberen unterzubringen, damit die Handspanne für schnelles Rechnen nicht überschritten wird wie bei zehn Kugeln, und fertig ist die Rechenhilfe. Alles andere macht der menschliche Geist.
Rechenaufgabe 234/6:
"Stelle den Divisor 6 ganz links und den Dividend 234 ganz
rechts auf der Maschine ein.
Versuche die erste Zahl des Dividenden (2) durch den Divisor 6 zu
teilen. Geht nicht!
Versuche die ersten beiden Ziffern des Dividenden 23 durch den
Divisor
6 zu teilen, ist gleich 3.
Stelle diese 3 links im Mittelfeld (mit einer Leersäule Abstand
vom
Divisor) ein.
Multipliziere diese 3 mit dem Divisor 6 und ziehe das Ergebnis 18
von
den 23 ab. Es bleiben rechts nun 54 übrig.
Teile diese restlichen 54 durch den Divisor 6. Das Ergebnis 9
stelle in
der Mitte ein, und zwar auf der Säule rechts neben der 3.
Multipliziere diese 9 mit dem Divisor 6. Das Ergebnis 6x9=54 ziehe
von
dem Rest des Dividenden 54 ab. Es bleibt kein Rest. Das
Endergebnis 39
ist in der Mitte abzulesen".
Alles klar? Der Japaner pflegt dem Vernehmen nach die Ergebnisse eines elektronischen Taschenrechners mal eben mit dem Abakus nachzurechnen, damit er sicher sein kann, dass es stimmt...
Link:
Walther WSR 160 Kurbelrechenmaschine 4-Spezies

Rechenbeispiele: Eine
Kurbelumdrehung = unten 1x addieren, was man oben eingestellt hat.
Drei Kurbelumdrehungen = 3x addieren. Die Kurbelumdrehungen werden
links unten mitgezählt, das Resultat rechts unten angezeigt.
1 Zehnerstelle nach links verstellen, 1 Kurbelumdrehung =
insgesamt mit
13 multiplizieren.
Auch
für Divison und Wurzelziehen ist die Maschine eingerichtet. Ihre
Innereien sind aus unverwüstlichem Messing-Guss und funktionierten
auch
nach 50 Jahren auf Anhieb.
Eine fantastische Anleitung zu dieser Maschine findet man unter http://www.rechenkasten.de/Walther/Documents/Manuals/WSR_160/index.html und auf der Website gibt es noch viel mehr Informationen über Walther und andere Rechenmaschinen.
Odhner-Kurbelrechenmaschine

Voll mechanisch und trotzdem druckend - nicht das Flair der Brunsviga Kurbelmaschinen aus Messing, aber doch schon ein gewohntes Design.

Solide Mechanik verleiht der Maschine eine unbegrenzte Lebensdauer ... und ein Gewicht von fast 5 kg.
Notiz für mich: "C" ist für "Eingabewiederholung"
Buchungsplatte
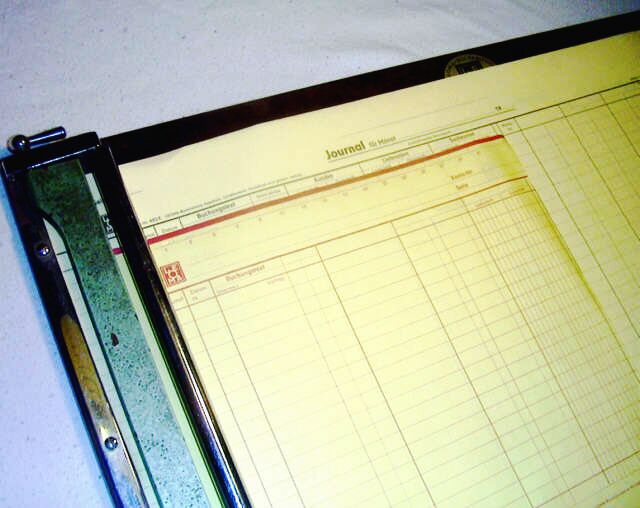
Erst mit der Verbreitung des "Blaupapiers" zum Durchschreiben von Hand wurde es möglich, mittels einer sinnreichen Klemmvorrichtung, getrennt für das Journal und die Kontenblätter, aus der reinen Übertragungsbuchführung die zuverlässigere Durchschreibebuchführung zu entwickeln. Hier eine Buchungsplatte von Leoma, Augsburg, mit einem eingelegten Kontenblatt für Sachbuchungen (Spalte ganz rechts).
Und dann war da noch A.E. van Vogt (1912-2000), "Mr. Science Fiction" persönlich, der 1952 in "Das Reich der 50 Sonnen (The Mixed Men)" seine damalige Version eines Taschenrechners beschrieb:
"Er setzte sich an sein Pult und zog sein Berufswerkzeug aus der Tasche: einen Rechenschieber mit einem daran befestigten Radiogerät, das ihn mit dem nächsten Elektronengehirn - in diesem Falle dem des Schiffes - verband." (Anmerkung: von bluetooth würde noch 50 Jahre lang niemand reden...).
Lesetipp: Spiegel-Artikel in "Einestages" vom 8. Januar 2009